У цьому розділі ми представляємо зібрані набори даних про несправності, моделі, що використовують для порівняння та модельні критерії порівняння. Ми також обговорюємо продуктивність моделей з використанням двох наборів даних несправностей із компонентів системи великих даних з відкритим кодом, і кожен набори даних несправностей включають три підгайні, зібрані з послідовних випущених компонентів системи великих даних з відкритим кодом.
Набори даних про несправності
У цій роботі ми використовуємо два набори даних про несправності, зібрані з двох різних компонентів системи великих даних з відкритим кодом – YARN та HDFS – у випуску систем відстеження, доступні за адресою https://issues.apache.org/. Існує три субдатази, зібрані з пряжі, такі як пряжа 0,23,5, пряжа 0,23,6 та пряжа 0,23,7. Існує три субдатази, зібрані з HDFS, такі як HDFS 3.1.1, HDFS 3.1.2 та HDFS 3.1.3.
Перший набір даних про несправності (DS1-1) з пряжі 0,23,5 включає 28 виявлених несправностей з використанням 29 тижнів з 3 травня 2012 року по 16 листопада 2012 року. У другому наборі несправностей (DS1-2) з пряжі 0.23.6 15 несправностей було виявлено протягом 48 тижнів з 22 лютого по 23 січня 2013 року. 7, 2011 р. По 12 березня 2013 р. У четвертому наборі даних про несправності (DS2-1) з HDFS 3.1.1, 84 несправності були виявлені протягом 47 місяців з 19 вересня 201 (DS2-3) З HDFS 3.1.3 69 несправностей було виявлено протягом 54 місяців з 17 квітня 2015 року по 2 жовтня 2019 року.
Зауважте, що типи несправностей у зібраних нами компоненти системи великих даних з відкритим кодом включають помилку, завдання та підсумки, але не вдосконалення, нову функцію, тест та бажання.
Причини полягають у наступному,
- 1.
Вдосконалення стосується лише вдосконалень або удосконалень на існуючі функції чи завдання, а не звітування про збої або проблеми системи.
- 2.
Нова функція посилається на функції або функції, заплановані для реалізації в майбутніх версіях програмного забезпечення, не повідомляючи про існуючі збої системи.
- 3.
Тест: Зазвичай використовується для відстеження тестування програмного забезпечення, пов'язаних завдань, тестових випадків та тестових планів. Це може включати в себе написання, виконання та управління тестовими випадками, а не звітуванням про збої системи.
- 4.
Бажання: зазвичай використовується для позначення бажання чи пропозиції щодо вдосконалення системи або нових функцій, а не повідомляти про помилки чи проблеми з існуючими системами.
Моделі для порівняння
Щоб провести ретельне порівняння продуктивності моделей, ми вибрали кілька SRMS. Ми використовуємо сім SRM для порівняння продуктивності підгонки та прогнозування, використовуючи шість наборів даних несправностей програмного забезпечення для великих даних з відкритим кодом. З таблиці 1 ми можемо побачити, що сім SRM включають модель Goel-Okumoto (GO), модель затримки S-подібної форми (DSS), модель перегину S-подібної форми, узагальнена модель GO (GGO), модель Zhang-Teng-Pham, модель LI та PM. У цих SRMS SRMS SRM включає модель GO, DSS, ISS, GGO та Zhang-Teng-Fam. SRM з відкритим кодом включають модель LI та PM. Ідеальна налагодження SRMS має GO, DSS, ISS, GGO, LI Model та PM. Модель Чжан-Тенг-Фем-це недосконала налагодження SRM.
Критерії порівняння моделі
Ми оцінюємо продуктивність моделі, використовуючи п’ять критеріїв порівняння моделі: наприклад, MSE, R2TS, MEOP та дисперсія. Вони можуть позначати наступним чином,
$$ mse = \ frac {{\ sum \ nolimits_ {j = 1}^{n} {(m (t_ {j}) – o _ {{t_ {j}}})^{2}}}} {n – \ theta} $$
(9)
де \ (m (t_ {j}) \) представляє очікувану кумулятивну кількість виявлених несправностей за часом tj. \ (O _ {{t_ {j}}} \) позначає фактичну кількість спостережуваних несправностей за часом tj. п. і \ (\ theta \) представляють розмір зразків та номер параметра моделі відповідно.
$$R^{2} = 1 – \frac{{\sum\nolimits_{j = 1}^{n} {(O_{{t_{j} }} – m(t_{j} ))^{2} } }}{{\sum\nolimits_{j = 1}^{n} {(O _ {{t_ {j}}} – \ sum \ nolimits_ {i = 1}^{n} {\ frac {{o _ {{t_ {i}}}} {n}})^{2}}}} $$
(10)
де в рівнянні. (10), \ (m (t_ {j}) \),\ (O _ {{t_ {j}}} \) і п. ідентичні тим, хто в рівнянні. (9).
$$ ts = \ sqrt {\ frac {{\ sum \ nolimits_ {j = 1}^{n} {(m (t_ {j}) – o _ {{t_ {j}}})^{2}}}} {{\ sum \ nolimits_}}}^{\ sum \ nolimit_ {j = 1} {O _ {{t_ {j}}}^{2}}}}} \ рази 100 \%$$
(11)
де в рівнянні. (11), \ (m (t_ {j}) \),\ (O _ {{t_ {j}}} \) і п. ідентичні тим, хто в рівнянні. (9).
$$MEOP = \frac{{\sum\nolimits_{j = 1}^{n} {{|}m(t_{j} ) – O_{{t_{j} }} {|}} }}{{n – \theta { + }1}}$$
(12)
де в рівнянні. (12), \ (m (t_ {j}) \),\ (O _ {{t_ {j}}} \), п. і \ (\ theta \) такі ж, як і у рівнянні. (9).
$$ \ start {вирівнюється} дисперсія & = \ sqrt {\ frac {{\ sum \ nolimits_ {j = 1}^{n} {(o _ {{t_ {j}} – m (t_ {j}) – bias)^{2}}}} {n -1}}} \ \},}}, \\ bias & = \ frac {{\ sum \ nolimits_ {j = 1}^{n} {(m (t_ {j}) – o _ {{t_ {j}}})}} {n} \\ \ end {Aligned} $$
(13)
де в рівнянні. (13), \ (m (t_ {j}) \),\ (O _ {{t_ {j}}} \) і п. такі ж, як і у рівнянні. (9).
Зауважте, що чим менші значення MSE, TS, MEOP та дисперсія, тим вище продуктивність моделі. Але більший r2 Цінність, тим краще пристосування моделі.
Для правильної оцінки та порівняння ефективності різних атрибутів SRMS ми використовуємо ранг (\ (Ncd_ {k} \)) метод з літератури17. \ (Ncd_ {k} \) можна позначити наступним чином,
$$ ncd_ {k} = \ sqrt {\ зліва ({\ sum \ limits_ {j = 1}^{n1} {\ зліва ({\ frac {{\ chi_ {kj}}} {{\ sum \ nolimits_ {i = 1}^{n2 {\ chi_ {ij}}}}} \ right)^{2} \ psi_ {j}}} \ right)}, \; \; \; \; \; k = 1,2, …, n2. $$
де п.1 і п.2 представляють кількість критеріїв порівняння моделі та кількість порівняння SRM відповідно. відповідно. \ (\ chi_ {kj} \) позначає стандартне значення kКритерії SRM та JTH.
\ (\ psi_ {j} \) являє собою вагу, коли індекс критерію є j. Менший \ (Ncd_ {k} \) Значення представляє кращу продуктивність моделі.
Результати та обговорення порівнянь моделей
Порівняння продуктивності моделі
Щоб перевірити точність та ефективність ПМ, ми порівняли продуктивність придатності з шістьма наборами несправностей та семи СРМ. У таблиці 2 перераховані значення оцінки параметрів ПМ за допомогою методу LSE для 100% та 90% DS1 та DS2 відповідно. Таблиця 3 вказує на те, що ПМ має відмінні продуктивність у порівнянні з іншими моделями. Наприклад, у таблиці 3, використовуючи 100% DS2-1, MSE, TS, MEOP моделі МКС, приблизно 5,25, 2,35 та 1,95 рази більше, ніж у ПМ відповідно. Використовуючи 100% DS2-2, MSE, TS та MEOP моделі МКС, майже в 5,43, 2,41 та 1,89 рази більше, ніж у ПМ, відповідно, таблиці 4. З таблиці 5 ми можемо чітко побачити результати рейтингу SRM. Перший рейтинг – Прем'єр -міністр, другий – модель МКС, а найгірша – модель GO. Порядок рейтингу інших SRMS не виправлений. Ці результати свідчать про те, що ПМ має кращі показники відповідності порівняно з іншими СРМ. Ці результати можна чітко видно з рис. 3. На малюнку 3 видно, що порівняння продуктивності пристосування восьми SRM за допомогою шести наборів даних несправностей. На малюнку 3 видно, що придатна продуктивність ПМ перевершує інші SRMS Рис. 4.
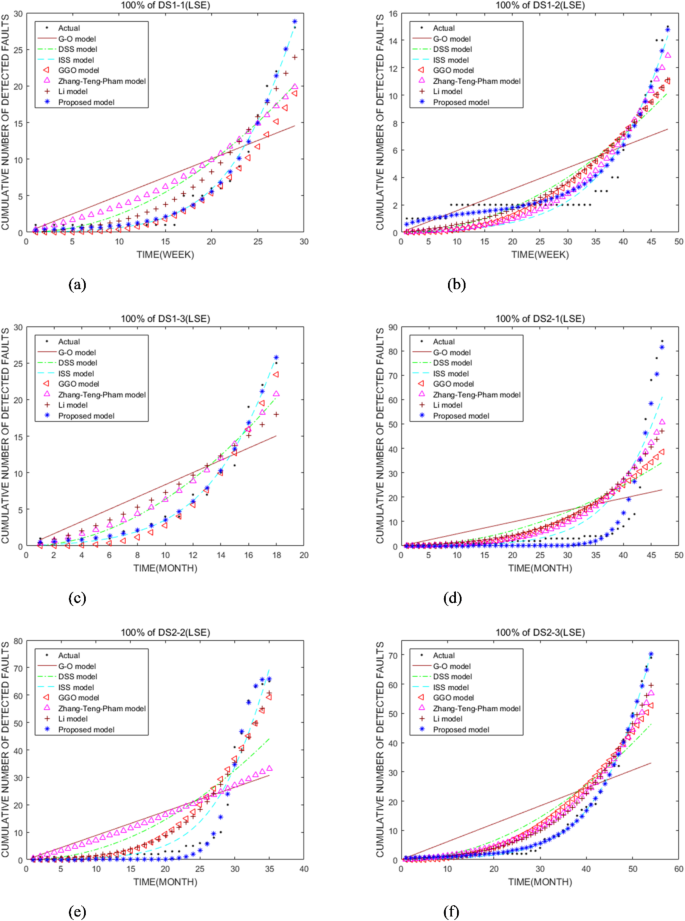
Порівняння продуктивності для SRMS з використанням 100% DS1 та DS2 відповідно. (–f) являє собою порівняння продуктивності для SRMS з використанням 100% DS1-1, DS1-2, DS1-3, DS2-1, DS2-2 та DS2-3 відповідно.
Ми провели 95% довірчий інтервал для ПМ за допомогою 100% наборів даних несправностей. З фіг. Це вказує на те, що значення оцінки параметрів ПМ є ефективними та стабільними. На рис. 5D, хоча є одна точка, яка виходить за межі інтервалу, загалом оцінені значення параметрів ПМ є прийнятними. Це вказує на складність встановлення SRM для програмного забезпечення для великих даних з відкритим кодом, однак, ПМ добре підходить для цієї ситуації.

Порівняння ефективності прогнозування для SRMS з використанням 90% DS1 та DS2 відповідно. (–f) являє собою порівняння прогнозних показників для SRMS з використанням 90% DS1-1, DS1-2, DS1-3, DS2-1, DS2-2 та DS2-3 відповідно.
Порівняння модельної прогнозної продуктивності
Для перевірки прогнозування ПМ ми провели відповідні експерименти. У таблиці 4 видно, що прогнозна продуктивність ПМ перевищує інші SRM, використовуючи 90% наборів даних несправностей, за винятком використання 90% DS2-2. Наприклад, у таблиці 4, використовуючи 90% DS1-3, MSE, TS, дисперсії та MEOP моделі МКС, приблизно 3,58, 1,89, 1,9 та 1,4 рази більше, ніж у ПМ. Використання 90% DS2-1, MSE, TS, дисперсії та MEOP моделі GGO приблизно в 7,19, 2,68, 2,52 та 3,18 разів більше, ніж у ПМ. З таблиці 6 ми можемо побачити, що модель PM, ISS та модель GO першим, другий та останній відповідно. У таблиці 4, використовуючи 90% DS1-1, значення дисперсії (0,4818) моделі МКС менше (0,5248) ПМ. Але з таблиці 6 очевидно, що прогнозна ефективність Прем'єр -міністра перевершує модель МКС через всебічні порівняння. Крім того, у таблиці 4, використовуючи 90% DS2-2, значення дисперсії та MEOP моделі МКС менше, ніж значення ПМ. Вони мають 2,1273 та 0,6264 для моделі МКС, а 2,3336 та 0,6564 для ПМ. У таблиці 6 видно, що перший рейтинг-це модель МКС, а другий-ПМ, що використовує 90% DS2-2. Однак значення ранжування ПМ близьке до моделі МКС.
Прогнозування продуктивності ПМ перевершує інші моделі. Як видно з таблиці 6, за винятком ПМ, прогностична продуктивність інших моделей не є стабільною. Наприклад, використовуючи 90% DS2-1, модель МКС займає третє місце, тоді як вона займає перше, використовуючи 90% DS2-2, а інша ситуація займає друге місце. Інші SRM мають ті самі зміни, що і модель МКС. Зауважте, що з таблиць 5 та 6 ми можемо побачити, що модель GO є найгіршою, використовуючи 100% або 90% наборів даних несправностей. Це вказує на те, що модель GO не підходить для оцінки надійності програмного забезпечення для великих даних з відкритим кодом. З рис. 4 ми бачимо, що ПМ найкращий серед усіх SRMS щодо прогнозних показників, використовуючи 90% наборів даних несправностей.
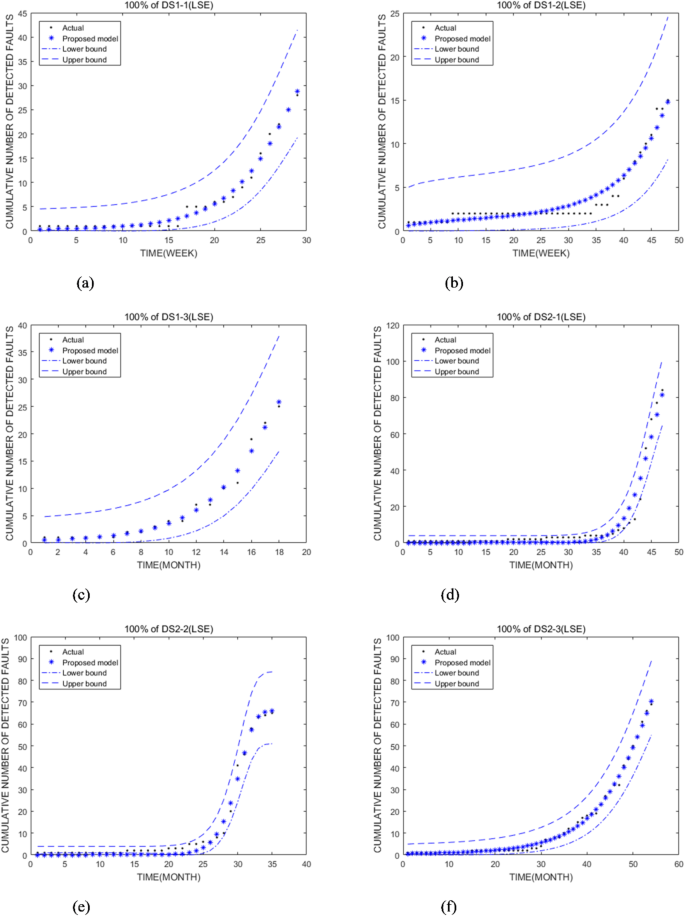
95% довірчий інтервал для запропонованої моделі з використанням 100% DS1 та DS2 відповідно. (–f) являє собою 95% довірчий інтервал для ПМ за допомогою 100% DS1-1, DS1-2, DS1-3, DS2-1, DS2-2 та DS2-3 відповідно.
Підводячи підсумок, ПМ має кращі придатні та прогностичні показники в процесі виявлення несправностей програмного забезпечення з великими даними з відкритим кодом. PM прогнозує найбільш точну кількість помилок у програмному забезпеченні та має найбільш стабільну продуктивність. Експеримент підтвердив, що виявлення несправностей програмного забезпечення програмного забезпечення для великих даних з відкритим кодом слідує за розподілом Weibull -Weibull та ефективністю ПМ у прогнозуванні несправностей у процесі тестування програмного забезпечення з великими даними з відкритим кодом.










